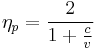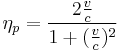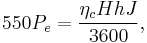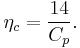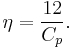Propulsive efficiency

In aircraft and rocket design, overall propulsive efficiency 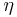$\eta$ is the efficiency, in percent, with which the energy contained in a vehicle's propellant is converted into useful energy, to replace losses due to air drag, gravity, and acceleration. It can also be stated as the proportion of the mechanical energy actually used to propel the aircraft. It is always less than 100% because of kinetic energy loss to the exhaust, and less-than-ideal efficiency of the propulsive mechanism, whether a propeller, a jet exhaust, or a fan. In addition, propulsive efficiency is greatly dependent on air density and airspeed.

Mathematically, it is represented as 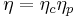$\eta = \eta_c \eta_p$ ^[1] where 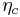$\eta_c$ is the cycle efficiency and 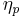$\eta_p$ is the propulsive efficiency. The cycle efficiency, in percent, is the proportion of energy that can be derived from the energy source that is converted to mechanical energy by the engine.

1 Estimation
2 See also
3 References
4 Notes

Estimation

Jet engines

For all airbreathing jet engines the propulsive efficiency (essentially energy efficiency) is highest when the engine emits an exhaust jet at a speed that is the same as, or nearly the same as, the vehicle velocity. The exact formula for air-breathing engines as given in the literature,^[2] is

$\eta_p = \frac{2}{1 %2B \frac{c}{v}}$

where c is the exhaust speed, and v is the speed of the aircraft.

A corollary of this is that, particularly in air breathing engines, it is more energy efficient to accelerate a large amount of air by a little bit than a small amount by a large amount, even though the thrust is the same. Note however, that duct jet engines give no thrust when the inlet and exhaust speeds are exactly the same.

Rocket engines

A rocket engine's 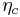$\eta_c$ is usually high due to the high combustion temperatures and pressures, and long nozzle employed. The value varies slightly with altitude due to atmospheric pressure on the outside of the nozzle/engine, but can be up to 70%. Most of the remainder is lost as heat energy in the exhaust.

Rocket engines have a slightly different propulsive efficiency (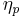 $\eta_p$ ) than airbreathing jet engines as the lack of intake air changes the form of the equation. This also means that rockets are able to exceed their exhaust velocity. See diagram.

$\eta_p= \frac {2 \frac {v} {c}} {1 %2B ( \frac {v} {c} )^2 }$ ^[3]

As with ducted jet engines, matching the exhaust speed and the vehicle speed gives optimum efficiency in principle. Although in practice rocket exhausts are high and typically fixed, this can be a useful theoretical consideration. Unlike ducted engines, rockets give thrust even when the two speeds are equal.

Rockets often also have an additional significant source of energy, because they are able to leverage the kinetic energy of their propellant with the Oberth effect. This is also a factor for air-breathing aircraft, but much smaller one due to their lower speed.

Propeller engines

The calculation is somewhat different for reciprocating and turboprop engines which rely on a propeller for propulsion since their output is typically expressed in terms of power rather than thrust. The equation for heat added per unit time, Q, can be adopted as follows:

$550 P_e = \frac{\eta_c H h J}{3600},$

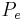where $P_e$ is engine output in horsepower, converted to foot-pounds/second by multiplication by 550. Given that specific fuel consumption is C_p = h/P_e and using the aforementioned substitutions for H and J, the equation is simplified to:

$\eta_c = \frac{14}{C_p}.$

expressed as a percentage.

Assuming a typical propulsive efficiency 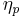$\eta_p$ of 86% (for the optimal airspeed and air density conditions for the given propeller design), maximum overall propulsive efficiency is estimated as:

$\eta = \frac{12}{C_p}.$

References

Loftin, LK, Jr.. "Quest for performance: The evolution of modern aircraft. NASA SP-468". http://www.hq.nasa.gov/pao/History/SP-468/cover.htm. Retrieved 2006-04-22.
Loftin, LK, Jr.. "Quest for performance: The evolution of modern aircraft. NASA SP-468 Appendix E". http://www.hq.nasa.gov/pao/History/SP-468/app-e.htm. Retrieved 2006-04-22.

Notes

^ ,ch10-3
^ K.Honicke, R.Lindner, P.Anders, M.Krahl, H.Hadrich, K.Rohricht. Beschreibung der Konstruktion der Triebwerksanlagen. Interflug, Berlin, 1968
^ George P. Sutton & Oscar Biblarz, Rocket Propulsion Elements, pg 37-38 (seventh edition)